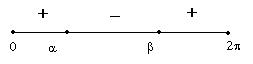
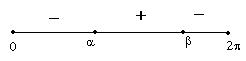
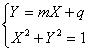Equazioni lineari
|
acos(x)+bsin(x)+c=0 |
|
Se c=0 |
|
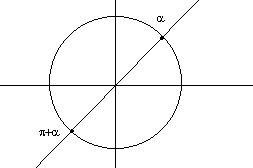
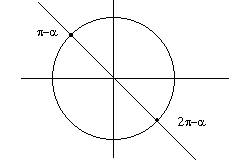
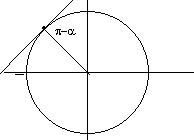
acos(x)+bsin(x)=0 tan(x)=(-b/a), x=atn(-b/a)+kp Tra [0,2p] a , p-a (oppure p+a, 2p-a )
|
|
Se c¹0 |
||
|
Pongo X=cos(x) Y=sin(x) Per cui l’equazione diventa aX+bY+c=0 Esplicitando Y=mX+q Mettendo a sistema con la circonferenza goniometria
Per cui con |
||
|
D<0 n.s. |
|
|
|
D=0 1 Sol. che ottengo risolvendo X1=X2=cos(x) Þ tra le soluzioni a ,2p-a , p-a , p+a necessariamente devo scegliere quella soluzione che interseca la retta. ( a=arccos(|X1|) |
|
|
|
D>0 2
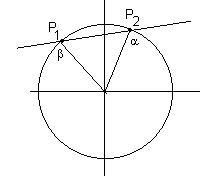
sol. X1 e X2 X1=cos(x) a , 2p-a , p-a ,p+a X2=cos(x) b , 2p-b,p-b,p+b delle 4 devo scegliere le
due soluzioni che intersecano la retta. a=arccos(|X1|) b=arccos(|X2|) |
|
|
Disequazioni Lineari
Per risolvere le disequazioni lineari: acos(x)+bsin(x)+c³0 :
|
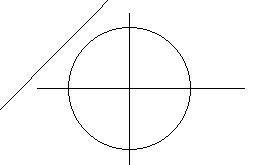
1) Rappresentare graficamente la retta : aX+bY+c=0 sulla circonferenza goniometria. |
||
|
2) Passare a risolvere l’equazione : acos(x)+bsin(x)+c=0 (Vedi sopra) |
||
|
3) discutere il sistema: Quando è che acos(x)+bsin(x)+c³0 ? |
||
|
Ricordando che se
b>0 |
Se b<0 |
|
|
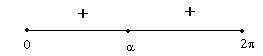
si ha che bsin(x)³ -acos(x)-c Þ sin(x)³ (-a/b)cos(x)-c/b Þ Y³ mX+q i valori positivi sono al disopra
della retta. |
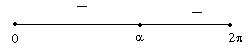
si ha che bsin(x)³ -acos(x)-c Þ sin(x) £ (-a/b)cos(x)-c/b Þ Y£ mX+q i valori positivi sono al
disotto della retta. |
|
|
Allora si possono presentare i seguenti casi |
||
|
Se D<0 oppure |
|
|
|
D=0 |
|
|
|
D>0 |
|
|
Esempi di Equazioni
Lineari:
1) 
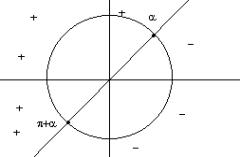
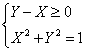
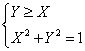
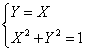
passando all’equazione per trovare i valori
di a
, 
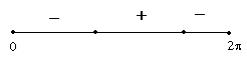
e 
allora 
2)
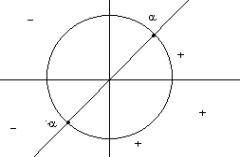
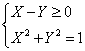
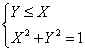
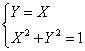
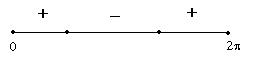
passando all’equazione
, 
e 
allora 
e 
3)
Studio la disequazione al positivo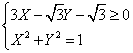
la disequazione
sarà positiva per valori sotto la retta.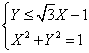
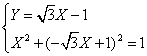
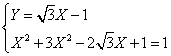
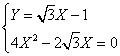
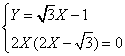da cui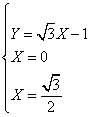 
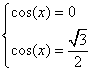
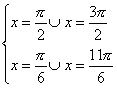
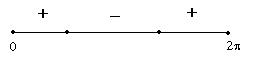
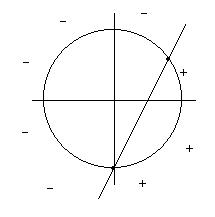
soluzione 
4)
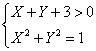la
disequazione sarà positiva per valori sopra
la retta.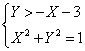
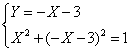
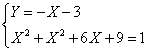
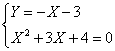
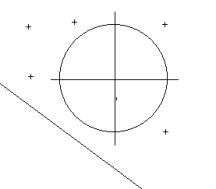
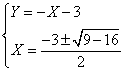delta minore di
zero, allora come si vede anche dal grafico funzine sempre positiva e allora il
risultato è per qualsiasi valore. "xÎ R
5)
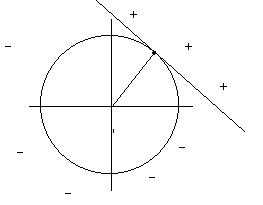
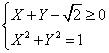la
disequazione sarà positiva per valori sopra
la retta. 
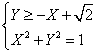
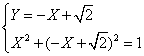
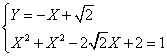
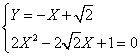
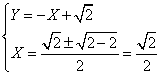da cui delta =0. Ho
un solo valore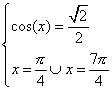 
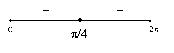
Soluzione 