Questionario:

Soluzione Maturità 2004 Pni

Problema 1

PROBLEMA 1

Sia la curva d'equazione:

ove e sono parametri positivi.

1. Si studi e si disegni ;

C.E. Curva simmetrica rispetto all’asse y

Positività: sempre verifica.

Intersezione con l’asse x: nessuna soluzione

Intersezione con l’asse y:

y=0 asintoto orizzontale

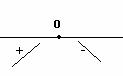
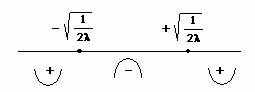
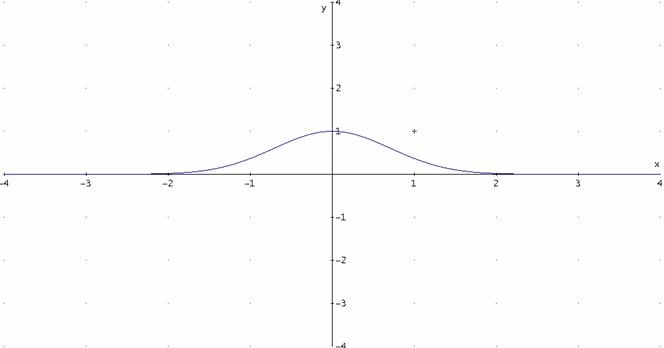
2. si determini il rettangolo di area massima che ha un lato sull'asse x e i vertici del lato opposto su ;

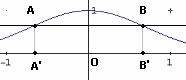Considerando il generico rettangolo ABA’B’. con

e .

massimo per

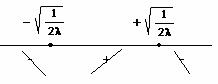Massimo per

3. sapendo che 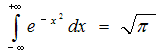Formula e assumendo , si trovi il valore da attribuire a affinché l'area compresa tra e l'asse x sia 1;

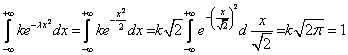da cui

4. per i valori di e sopra attribuiti, è detta curva standard degli errori o delle probabilità o normale di Gauss (da Karl Friedrich Gauss, 1777-1855). Una media e uno scarto quadratico medio come modificano l'equazione e il grafico?

L’equazione generale della gaussiana diventa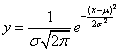

L’andamento grafico dell’equazione generale è lo stesso della curva standard. Quello che cambia è la posizione dell’asse di simmetria e le dimensioni della curva. In parole povere ho sempre la forma tipica a “campana” posizionata diversamente e dilatata nel piano.

Come si vede la funzione ha lo stesso C.E.

La curva diventa simmetrica rispetto a

L’intersezione con l’asse x diventa 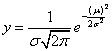. Stesso asintoto orizzontale

Derivata: 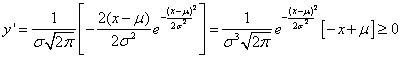e quindi massimo nel punto

Praticamente il valore di trasla in grafico nella direzione dell’asse x. E il valore di dilata il grafico.

Con un opportuna traslazione e dilatazione si può tornare alla curva standard

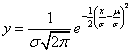in fatti posto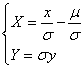

Si osserva che il determinate di suddetta trasformazione e quindi l’area o porzioni d’area sottese nelle curve gaussiane e l’area o porzioni d’area corrispondenti nella curva standard sono uguali. Infatti il rapporto di aree in una trasformazione affine è uguale al determinate della trasformazione

Per esempio, variando , assegnandoli valori come e si ha:

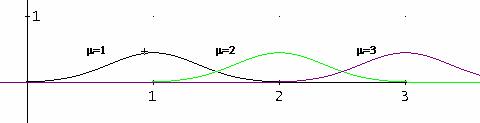
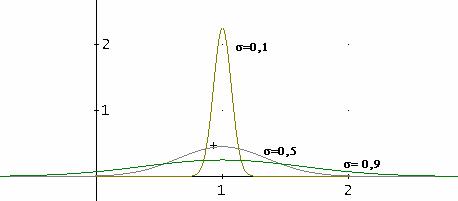
Per esempio variando , assegnandoli valori e si ha:

Problema 2

poiché f(x) è continua nell’intervallo se m e M sono il minimo e il massimo assoluto in questo intervallo allora allora per un la continuità la funzione assume tutti i valori

tra m e M e quindi anche il valore che è compreso tra a e b.

Osserviamo che la funzione è dispari dato che

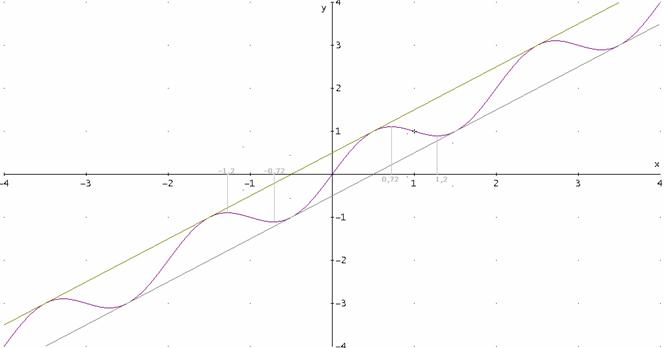
ed inoltre la funzione f(x) è compresa tra le due rette dato che al massimo il seno può valere 1 o -1.

C.E.

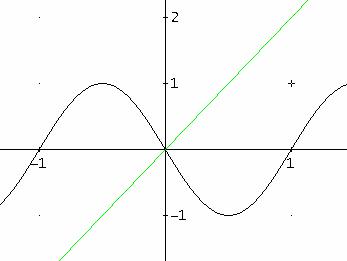Graficamente si vede che

per

Quindi intersezione con gli assi O(0,0)

La funzione non ha asintoti verticali , orizzontali o obliqui.

dove k numero intero qualsiasi.

dato che e quindi

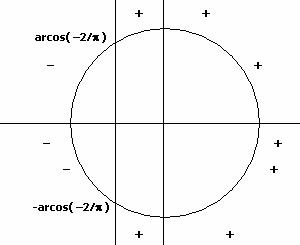quindi

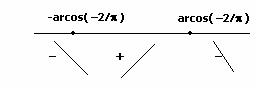ho un massimo per e minimi per

Massimi:

Minimi:

Per k=0

Per k=1

Per k=-1

da cui da cui

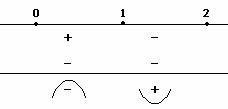
in generale si hanno flessi per

Utilizziamo il metodo di bisezione applicato nell’intervallo

n	a	b	m	fa	fb	fm
0	0	1	0,5	2,570796	-0,5708	1
1	0,5	1	0,75	1	-0,5708	-0,11072
2	0,5	0,75	0,625	1	-0,11072	0,398882
3	0,625	0,75	0,6875	0,398882	-0,11072	0,127312
4	0,6875	0,75	0,71875	0,127312	-0,11072	0,003497
5	0,71875	0,75	0,734375	0,003497	-0,11072	-0,05488
6	0,71875	0,734375	0,726563	0,003497	-0,05488	-0,026

Da cui soluzione x=0,726563

Questionario:

Quesito 1)

· L’angolo sessagesimale è la 360 parte dell’angolo giro, i sottomultipli sono i primi (1/60 di grado), i secondi (1/60 di minuto), e poi la divisione continua in decimi centesimi ecc.

· Preso un’angolo di una circonferenza di raggio 1, la misura dell’angolo in radianti corrisponde alla lunghezza dell’arco di tale angolo.

Vale la seguente proporzione dove x sono gli angoli misurati in radianti e alfa gli angoli misurati in gradi sessagesimali

· L’angolo è centesimale corrisponde alla centesima parte dell’angolo retto. Vale la seguente proporzione dove y sono gli angoli centesimali e alfa sono gli angoli sessagesimali.

Quesito 2)

Dato che la superficie di una Sfera di raggio R vale e dato che la superficie totale di un cilindro di raggio r vale e dato che allora

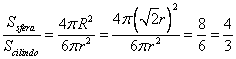
Quesito 3)

Una similitudine è un’affinità tale che il rapporto tra due segmenti corrispondenti vale k (k rapporto di similitudine).

Allora il volume varia come e l’area come e quindi . Se V’ è il volume trasformato e V il volume iniziale .

Se A’ è la superficie trasformata e S la superficie iniziale .

Quesito 4)

Le funzioni sono 81, ovvero Le disposizione con ripetizione di n oggetti su k posti.

Quesito 5)

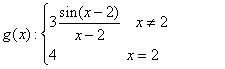Quesito 6)

Quesito 7)

I triangoli di assegnata base AB, e di uguale area hanno la stessa altezza h . Il problema è simmetrico. Il vertice C si trova sempre sulla retta parallela che non contiene AB. Per ogni triangolo ABC’, se ne trova un altro ABC’’ simmetrico rispetto all’asse OC.

La figura simmetrica di se stessa è il triangolo isoscele ABC, ed è in triangolo avente perimetro minimo.

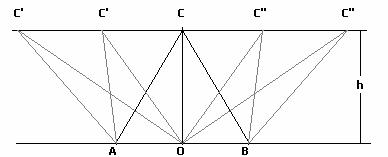
Oppure considerando un opportuno sistema di assi cartesiani dove O(0,0) C(x,h) e A(-a,0) B(a,0)

Si ha che dove

Derivando da cui

da cui

da cui e quindi x=0.

E per x=0 il triangolo ABC diventa isoscele

Quesito 8)

dividendo tutto per ab si ha che da cui

posto e si ha e se per esempio ho che e quindi due valori sono

Quesito 9)

la è crescente infatti per qualsiasi x, inoltre è definita per ogni x, ed è continua.

Ora dato che ,

la funzione necessariamente, per i teoremi sulla continuità, ammette un solo valore di x per cui f(x)=0.

Tramite il metodo di bisezione, nell’intervallo

n	a	b	m	fa	fb	fm
0	-1	0	-0,5	-2,63212	1	-0,89347
1	-0,5	0	-0,25	-0,89347	1	0,028801
2	-0,5	-0,25	-0,375	-0,89347	0,028801	-0,43771
3	-0,375	-0,25	-0,3125	-0,43771	0,028801	-0,20588
4	-0,3125	-0,25	-0,28125	-0,20588	0,028801	-0,08891
5	-0,28125	-0,25	-0,26563	-0,08891	0,028801	-0,03015
6	-0,26563	-0,25	-0,25781	-0,03015	0,028801	-0,0007

Da cui soluzione x=-0,2578

Quesito 10)

Considerato l’affinità generale

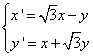
Prima di tutto si tratta di un’affinità con . (Trasformazione diretta)

E poiché la trasformazione soddisfa la condizione si tratta di una similitudine di rapporto

In conclusione si tratta di una similitudine diretta e quindi di una rotazione di centro (0,0) e angolo uguale a 30°.

Infatti considerato le rotazioni di centro O(0,0)