A.
S. 1999/2000
BRST - ESAME DI
STATO DI LICEO SCIENTIFICO
Indirizzo:
SCIENTIFICO TECNOLOGICO
– Progetto “BROCCA”
CORSO SPERIMENTALE
Tema di: MATEMATICA
Il candidato scelga a suo piacimento due dei seguenti problemi e li
risolva:
1. Sia f(x) una funzione reale
di variabile reale tale che valgano le seguenti condizioni:
f (x0) > 0
, f ’(x0) > 0 , f ”(x0) = 0 ,
dove x0 è un
particolare valore reale.
a) Spiegare perché tali condizioni non sono sufficienti a determinare l’andamento di f(x) in un intorno di x0.
Tali condizioni non sono sufficienti perché non sappiamo se in f ”(x0) = 0, c’è un flesso o la concavità verso l’alto, questo me lo dice la derivata terza. Infatti:
Se f ‘’(x0) = 0 e se f ‘’’(x0) ≠ 0 , ho un flesso
Se f ‘’(x0) = 0 e se f ‘’’(x0) =0, f IV(x0) ≠ 0 , ho la concavità verso l’alto o verso il basso.
b) Trovare almeno tre funzioni polinomiali f(x), di grado superiore al 1°, aventi andamenti diversi in x0 = 0, tali che:
f (0) = 1 , f ’(0) = 1 , f ”(0) = 0 .
1)![]()
![]()
![]()
2) ![]()
![]()
![]()
3) ![]()
![]()
![]()
c) Determinare, se possibile, tutte le rette tangenti ai grafici delle funzioni trovate e parallele alla retta di equazione y = x + 1.
1) ![]() da cui solo per
da cui solo per
![]() e allora
e allora ![]() da cui
da cui ![]()
![]()
2) ![]() da cui solo per
da cui solo per
![]() e allora
e allora ![]() da cui
da cui ![]()
![]()
3) ![]() da cui solo per
da cui solo per
![]() e allora
e allora ![]() da cui
da cui ![]()
![]()
d) A completamento del problema dimostrare la formula che esprime la derivata, rispetto ad x, della funzione xn, dove n è un intero qualsiasi non nullo.
Si può dimostra per induzione:
per n=0 ![]()
![]()
per n=1 ![]()
![]()
per
n=2 ![]()
![]()
Supposto vero per n-1 dimostriamolo per n
![]() ho che (proprietà
della moltiplicazione)
ho che (proprietà
della moltiplicazione) ![]()
oppure
con il rapporto incrementale ![]() considerando che
considerando che ![]() e quindi tutti i
termini h superiore al secondo grado vanno a zero
e quindi tutti i
termini h superiore al secondo grado vanno a zero
2. Nel piano, riferito ad un sistema monometrico
di assi cartesiani ortogonali (Oxy), sono assegnati i punti: A(0, 2), B(1, 1),
C(1, 0).
a) Trovare l’equazione della
circonferenza g inscritta nel triangolo
OAB.
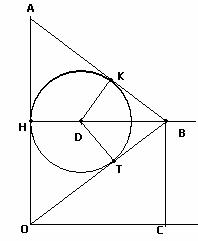
La circonferenza deve essere
tangente ai lati dei triangolo OAB. Allora per simmetria, dato che il triangolo
è isoscele ha l’ordinata del centro uguale a 1.
allora ![]()
Per
determinare ![]() imponiamo che
imponiamo che ![]() (raggi della
circonferenza) inoltre osserviamo
che
(raggi della
circonferenza) inoltre osserviamo
che ![]() e che la retta per OB
ha equazione
e che la retta per OB
ha equazione ![]() Allora
Allora ![]() da cui
da cui ![]()
Risolvendo ![]() da cui
da cui ![]() e
e ![]() che è negativa e si
scarta.
che è negativa e si
scarta.
La
circonferenza è allora ![]()
b) Determinare le equazioni
dell’affinità a che ha come punti uniti i
punti O e C e trasforma il punto B nel punto A.
![]()
![]()
![]() da cui p=0 e q=0
da cui p=0 e q=0
![]()
![]() da cui a=1 e c=0
da cui a=1 e c=0
![]()
![]() da cui b=-1 e d=2
da cui b=-1 e d=2
allora ![]()
c) Calcolare l’area del
triangolo CAA’, dove A’ è il punto trasformato di A nell’affinità a.
A’ ha coordinate ![]()
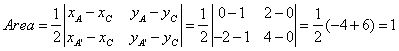
d) Stabilire se l’affinità a ha altri punti uniti, oltre ad O e C, e
trovare le sue rette unite.
![]()
![]()
![]() otteniamo una rette di
punti uniti
otteniamo una rette di
punti uniti
![]() si trasforma in
si trasforma in ![]() e quindi
e quindi ![]()
le
due rette saranno unite quando![]() dalla seconda
otteniamo che b=a e allora sono unite le rette
dalla seconda
otteniamo che b=a e allora sono unite le rette
![]() ovvero
ovvero ![]()
e) Stabilire quali, fra le
rette unite trovate, risultano tangenti o esterne a g .
La retta y=0 è sicuramente esterna a g . in vece le rette unite saranno secanti, tangenti o esterne a seconda che la distanza dal centro sia minore , uguale o maggiore del raggio.
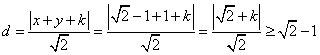
![]()
![]() e
e ![]() e quindi soluzioni
e quindi soluzioni ![]() e
e ![]()
3.
Assegnata la funzione:
![]()
dove il logaritmo si intende in base e, il candidato:
a)
determini per quali valori di a e b la f(x) ha un
minimo relativo nel punto (![]() ;
;
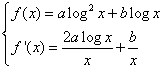 da cui
da cui 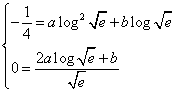 da cui
da cui 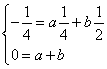
![]()
![]()
![]()
b) disegni la curva grafico della f(x) per i valori di a e di b così ottenuti e calcoli l’area della regione finita da essa delimitata con l’asse x.
![]()
Campo di esistenza x>0
Positività ![]() da cui
da cui ![]() da cui
da cui ![]()
![]() x=0 asintoto
orizzontale
x=0 asintoto
orizzontale
![]() scartando i termini di
grado inferiore
scartando i termini di
grado inferiore
![]()
![]()
![]() minimo.
minimo.
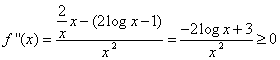 da cui
da cui ![]()
![]() concavità
positiva e flesso per
concavità
positiva e flesso per ![]()
![]()
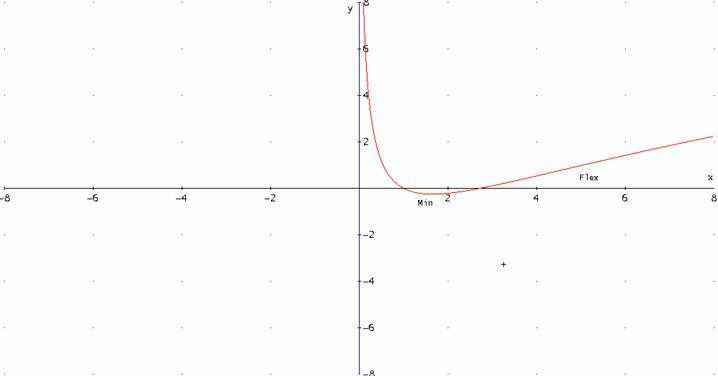
Abbiamo già visto che interseca l’asse x in 1 e in e.
Allora l’area
richiesta è ![]()
![]()
![]()
allora
![]()
![]()
e siccome è negativa
l’integrale vale ![]()
Calcoli infine la probabilità che lanciando un dado cinque volte, esca per tre volte lo stesso numero.
Se un evento ha probabilità p e devo calcolare la propabilità che quell’evento accada k volte su un n possibilità si usa la seguente formula
![]() . Se per esempio devo
calcolare la probabilità che esce 1 tre volte su 5 lanci. Considero che la
probabilità che esce 1 è
. Se per esempio devo
calcolare la probabilità che esce 1 tre volte su 5 lanci. Considero che la
probabilità che esce 1 è ![]() allora
allora 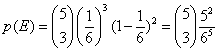 siccome per avere la
propabilità rischesta devo moltiplicare per 6.
siccome per avere la
propabilità rischesta devo moltiplicare per 6.
![]()