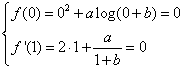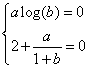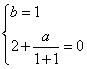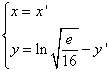A.
S. 2000/2001
Y557 - ESAME DI
STATO DI LICEO SCIENTIFICO
CORSO SPERIMENTALE
Tema di: MATEMATICA
La prova richiede lo svolgimento di uno dei due problemi proposti e le
risposte a cinque domande scelte all’interno del questionario.
PROBLEMA 1
Sia AB un
segmento di lunghezza 2a e C il suo punto medio.
Fissato un conveniente sistema di coordinate
cartesiane ortogonali monometriche (x, y):
a)
si verifichi che il luogo dei punti P
tali che ![]() = k (k costante positiva
assegnata) è una circonferenza (circonferenza di Apollonio) e si trovi
il valore di k per cui la soluzione
degenera in una retta;
= k (k costante positiva
assegnata) è una circonferenza (circonferenza di Apollonio) e si trovi
il valore di k per cui la soluzione
degenera in una retta;
b)
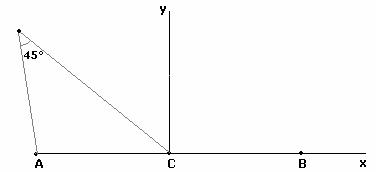
si determini il luogo geometrico g dei punti X che vedono AC sotto un angolo di 45°;
c)
posto X, appartenente a g , in uno dei due semipiani
di origine la retta per A e per B e indicato con a l’angolo ![]() si illustri
l’andamento della funzione y = f(x)
con f(x) = (XB / XA)2
si illustri
l’andamento della funzione y = f(x)
con f(x) = (XB / XA)2
e x = tga.
Soluzione problema 1:
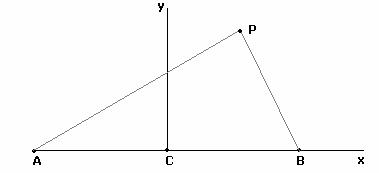
Posto il sistema di assi in modo che AB coincida con
l’asse x e l’asse y passi per C.
Si ha che
A(-a,0) C(0,0) e B(a,0). Da cui
![]()
![]() da cui
da cui  da cui
da cui
![]() e quindi
e quindi ![]()
![]()
![]()
il valore degenere è per k=1 e la retta diventa ![]() circonferenza di
centro
circonferenza di
centro 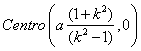
e raggio
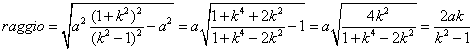
Le rette per c hanno equazione ![]() le rette per A hanno
equazione
le rette per A hanno
equazione ![]()
Poiché ![]() da cui
da cui 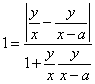 da cui
da cui 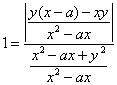 da cui
da cui
![]() da cui
da cui ![]() Circonferenze di
centro
Circonferenze di
centro ![]() e
e ![]() e raggio
e raggio
![]()
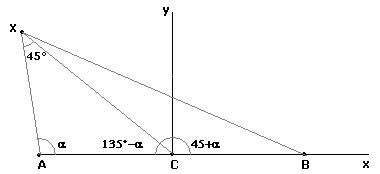
Osservando la figura sopra abbiamo che (Teorema dei
seni) 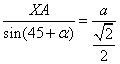 da cui
da cui
![]() e
e 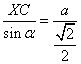 da cui
da cui ![]()
Per il teorema di Carnot applicato A XCB abbiamo che
![]()
e quindi ![]()
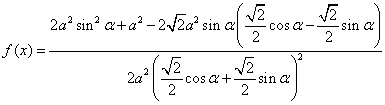
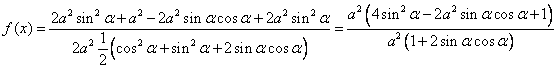
dividendo sopra e sotto per ![]() e considerando che
e considerando che ![]() abbiamo che
abbiamo che
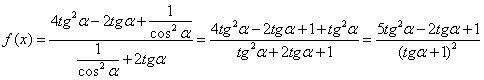
![]()
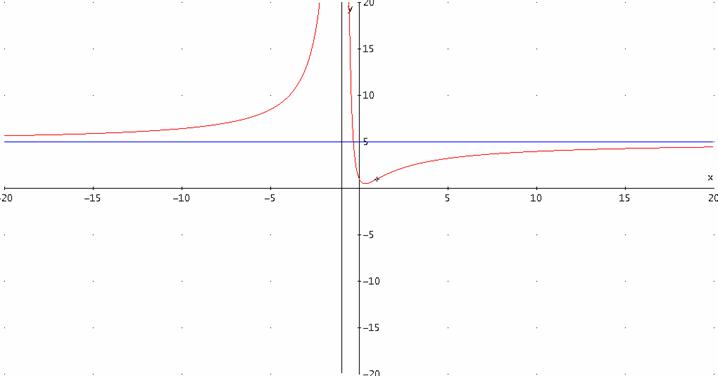
C.E. ![]()
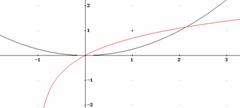
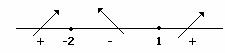
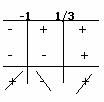
Positività ![]() per
per ![]() sempre positiva e mai
nulla
sempre positiva e mai
nulla
![]()
![]() AV x=1
AV x=1
![]() AO y=5
AO y=5
Derivata
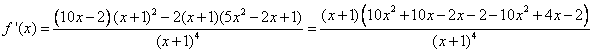
![]()
![]()
Intersezione con i propri asintoti ![]() da cui
da cui ![]() da cui
da cui ![]()
![]()
PROBLEMA 2
Nel piano riferito a coordinate cartesiane
ortogonali monometriche (x, y), è assegnata la funzione:
![]()
con a e b diversi da zero.
a) si trovino i valori di a e b tali che la curva G grafico della funzione passi per l’origine degli assi e presenti un minimo assoluto in x=1;
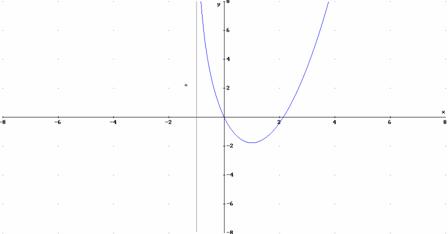
b) si studi e si disegni G;
c) si determini, applicando uno dei metodi numerici studiati, un’approssimazione della intersezione positiva di G con l’asse x;
d) si determini l’equazione della curva G’ simmetrica di G rispetto alla retta y = y(1);
e) si disegni, per i valori di a e b trovati, il grafico di:
![]()
Problema 2
Nel piano è assegnata la
funzione ![]() con a e b diversi da
zero.
con a e b diversi da
zero.
a) si trovino i valori di a e b che la curva G grafico della funzione passi per l’origine degli
assi e presenti un minimo assoluto in x=1.
|
|
b) Si studi e si disegni G
|
C.E. x>-1 A.V. x=-1 Positività o intersezione con gli assi. Come si deve
il limite della derivata
prima tende all’inifinto ( quindi non mi aspetto flessi).
|
c) Si determini, applicando uno dei metodi numerici
studiati un’approssimazione della intersezione della intersezione positiva di G con l’asse.
|
Occorre trovare due
valori a e b per cui f(a)f(b)<0.
Dal grafico a=1 e b=3 . f(1)=-1,77
f(3)=3,45
Soluzione circa x= 2,14 |
d) Si determini l’equazione della curva G’ simmetrica di G rispetto alla retta y=y(1)
|
Considerando la simmetria
assiale |
e) Si disegni per i valori di a e b trovati il grafico
di ![]()
|
|
Y557 - ESAME DI
STATO DI LICEO SCIENTIFICO
PIANO NAZIONALE DI INFORMATICA
CORSO SPERIMENTALE
Tema di: MATEMATICA
QUESTIONARIO
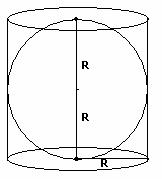
1. Provare che una sfera è equivalente ai 2/3 del cilindro circoscritto.
Se la sfera è di raggio
r. il raggio del cerchio di base è r el
‘altezza 2r.
Allora
![]()
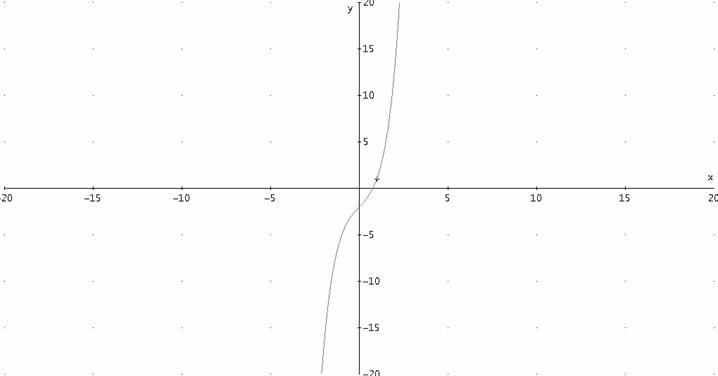
2. Determinare il numero delle soluzioni dell’equazione:
![]()
![]()
![]()
![]() sempre crescente.
sempre crescente.
![]()
![]()
siccome è sempre crescente e va da meno infinito a più infinito, la soluzione è unica.
3.
Dimostrare che se p(x)
è un polinomio, allora tra due qualsiasi radici distinte di p(x) c’è una radice di ![]() .
.
Se p(x) è un polinomio e se a e b sono due radici cioè
p(a)=p(b) allora applicando il teorema di Rolle all’intervallo [a,b] ho che
esiste un punto c per cui p’(x)=0
4. Calcolare la derivata della funzione
![]()
![]()
Quali conclusioni se ne possono trarre per la f(x)?.
Poiché la derivata è sempre nulla per un corollario al teorema di Lagrange la funzione è costante.
5. Calcolare l’integrale
![]()
6. Con uno dei metodi di quadratura studiati, si calcoli un’approssimazione dell’integrale definito

e si confronti il risultato ottenuto con il valore esatto dell’integrale.
Usiamo il metodo dei rettangoli o dei trapezi.
Sia ![]() e
e ![]() prendiamo 10 divisioni
quindi n=10
prendiamo 10 divisioni
quindi n=10
![]()
|
x |
f(x) |
|
0 |
0 |
|
0,314159 |
0,309017 |
|
0,628319 |
0,587785 |
|
0,942478 |
0,809017 |
|
1,256637 |
0,951057 |
|
1,570796 |
1 |
|
1,884956 |
0,951057 |
|
2,199115 |
0,809017 |
|
2,513274 |
0,587785 |
|
2,827433 |
0,309017 |
|
3,141593 |
1,23E-16 |
|
|
|
|
|
|
|
s= |
1,983524 |
|
S= |
1,983524 |
|
|
|
|
|
|
|
Int= |
0,991762 |
7.
Verificato che l’equazione![]() ammette una sola radice positiva compresa tra 0 e 1 se
ne calcoli un’approssimazione applicando uno dei metodi numerici studiati.
ammette una sola radice positiva compresa tra 0 e 1 se
ne calcoli un’approssimazione applicando uno dei metodi numerici studiati.
![]()
![]() Sempre positiva e quindi sempre crescente poiché
Sempre positiva e quindi sempre crescente poiché
![]()
![]() e quindi la
funzione è sempre crescente in zero è negativa e in 1 è positiva allora la
soluzione è unica e sta tra 0 e 1.
allora tramite il metodo di bisezione abbiamo che:
e quindi la
funzione è sempre crescente in zero è negativa e in 1 è positiva allora la
soluzione è unica e sta tra 0 e 1.
allora tramite il metodo di bisezione abbiamo che:
|
Soluzione circa x=0,57
|
8. Una classe è composta da 12 ragazzi e 4 ragazze. Tra i sedici allievi se ne scelgono 3 a caso: qual è la probabilità che essi siano tutti maschi?

9. Spiegare il significato di sistema assiomatico con particolare riferimento alla sistemazione logica della geometria.
Quesito 9
Il tema richiede una trattazione piuttosto lunga e
complessa. Un’esposizione in poche righe
può essere la seguente.
In un sistema assiomatico-deduttivo, dimostrare un teorema
significa verificare che esso
discende logicamente da un sistema di proposizioni precedentemente dimostrate, le quali
a
loro volta devono discendere da altre proposizioni. E’
evidente che questo procedimento deve
necessariamente avere un punto di
partenza. Devono quindi esserci un certo numero di
proposizioni, dette postulati o assiomi, che devono essere
accettate come vere e per le quali
non si può richiedere una dimostrazione.
Gli assiomi possono essere scelti in modo arbitrario, devono
però essere
• compatibili, cioè non si possono dedurre teoremi
che se si contraddicono,
• completi, cioè dagli assiomi scelti si devono poter
dedurre tutti i teoremi del sistema,
• indipendenti, cioè nessun assioma può essere
dimostrato come conseguenza degli altri
assiomi.
Nell’organizzazione logico-deduttiva che Euclide ha dato alla geometria nei suoi Elementi
(300 a.C.), assiomi e postulati fanno riferimento
a fatti intuitivamente evidenti o ad astrazioni
di
oggetti concreti.
L’assiomatica moderna, che nasce con
il libro del 1889 Fondamenti di Geometria
del
matematico tedesco D. Hilbert, la geometria è strutturata
come puro calcolo logico che opera
su un sistema di assiomi, senza alcun riferimento
al significato fisico-geometrico degli
assiomi stessi.
All’organizzazione logica della matematica hanno contribuito
in modo significativo anche G.
Peano, G. Frege e
B. Russell.
10. Dire, formalizzando la questione e utilizzando il teorema del valor medio o di Lagrange, se è vero che: «se un automobilista compie un viaggio senza soste in cui la velocità media è 60 km/h, allora almeno una volta durante il viaggio il tachimetro dell’automobile deve indicare esattamente 60 km/h».
![]() poiché il
significato geometrico del teorema di lagrange afferma che esiste almeno un
punto c della curva in a e b tale che direzione della tangente in c è uguale
alla direzione della corda per f(b) e f(a). e dato che il un diagramma orario la corda rappresenta
la velocità media nel tratto a e b e la
tangente la velocità istantanea in c, allora per il teorema di Lagrange esiste
un istante per cui l’automobile ha raggiungo il 60 Km/h.
poiché il
significato geometrico del teorema di lagrange afferma che esiste almeno un
punto c della curva in a e b tale che direzione della tangente in c è uguale
alla direzione della corda per f(b) e f(a). e dato che il un diagramma orario la corda rappresenta
la velocità media nel tratto a e b e la
tangente la velocità istantanea in c, allora per il teorema di Lagrange esiste
un istante per cui l’automobile ha raggiungo il 60 Km/h.
___________________________
Durata massima della prova: 6 ore.
È consentito l’uso della calcolatrice tascabile non programmabile e la consultazione del vocabolario di italiano.
Non è consentito lasciare l’Istituto prima che siano trascorse 3 ore dalla dettatura del tema.