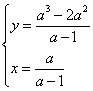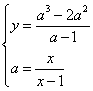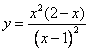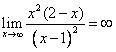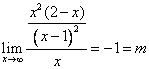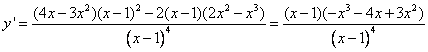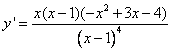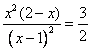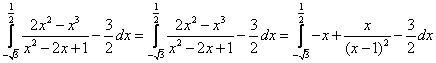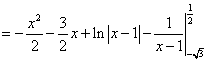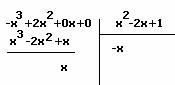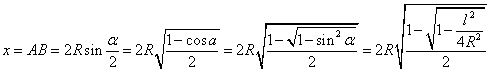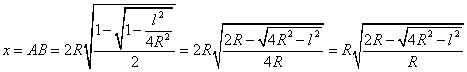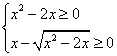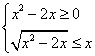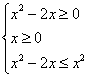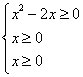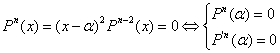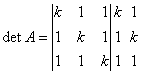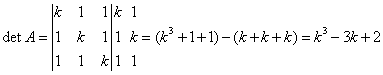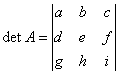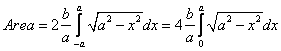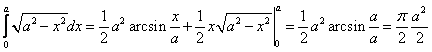ESAME DI STATO DI LICEO
SCIENTIFICO
a.s. 2002/2003
CORSO SPERIMENTALE
PNI e Progetto Brocca
SESSIONE SUPPLETIVA
Il candidato risolva uno dei due problemi e 5 dei 10
quesiti in cui si articola il questionario.
PROBLEMA 1.
In un piano, riferito ad un sistema di assi cartesiani
ortogonali (Oxy), sono assegnate le parabole di equazione:
y = (a – 1) x2 – 2 a x
+ a2 ,
dove a è un parametro reale diverso da 1.
|
a) Determinare quali tra esse hanno punti in comune con l’asse x e
quali no.
b) Trovare le due parabole che hanno il vertice in un punto di ascissa
a.
c) Stabilire se le due parabole trovate sono congruenti o no, fornendo
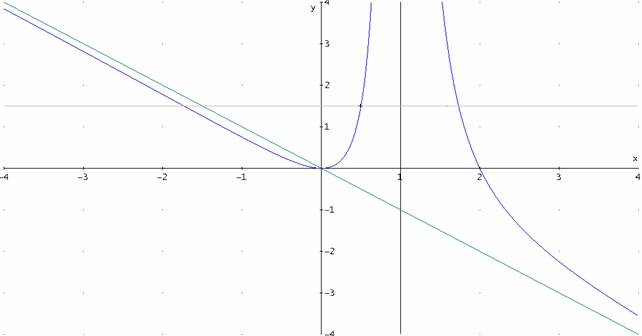
un’esauriente spiegazione della risposta. Le due parabole d) Scrivere l’equazione del luogo geometrico L dei vertici delle
parabole assegnate e disegnarne l’andamento dopo averne determinato in
particolare asintoti, estremi e flessi.
Luogo:
C.E.
derivata
e) Calcolare l’area della regione finita di piano delimitata dalla
curva L e dalla retta di equazione y=
|
PROBLEMA 2.
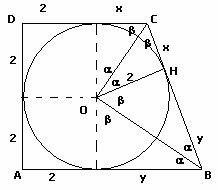
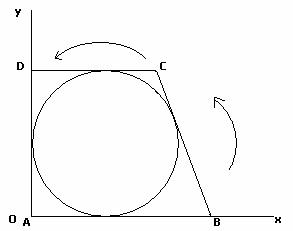
In un trapezio rettangolo ABCD, circoscritto ad un
cerchio, AB è la base maggiore, CD la minore e BC il lato obliquo. Le misure,
considerate rispetto alla stessa unità di misura, del raggio del cerchio e del
perimetro del trapezio sono nell’ordine 2 e 18.
![]()
![]() e per il teorema di
Euclide applicato al triangolo rettangolo OCB. Il triangolo è rettangolo poiché
ogni tangente è perpendicolare al raggio (del cerchio inscritto) e perchè
CO e OB bisecano gli angoli DCB e CBA.
(Vedi figura)
e per il teorema di
Euclide applicato al triangolo rettangolo OCB. Il triangolo è rettangolo poiché
ogni tangente è perpendicolare al raggio (del cerchio inscritto) e perchè
CO e OB bisecano gli angoli DCB e CBA.
(Vedi figura)
Allora ![]() da cui
da cui 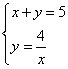
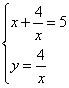
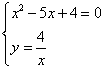 da cui
da cui ![]() e quindi x=1 y=4
e quindi x=1 y=4
|
a) Calcolare le misure dei lati del trapezio.
b) Riferito il piano della figura ad un conveniente sistema di assi
cartesiani (Oxy), scrivere le coordinate dei vertici del trapezio. c) Tra le centro-affinità di equazioni: |
x’ =
a x + b y , y’ = c x + d y ,
trovare quella che trasforma il vertice B del trapezio nel
vertice C e il vertice C nel vertice D.
![]()
![]() D(0,4) C(3,4)
D(0,4) C(3,4)
![]() B in C
B in C ![]() da cui
da cui ![]()
C in D ![]()
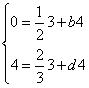
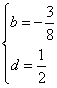
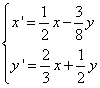 punti uniti
punti uniti 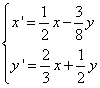
![]() da cui
da cui ![]() punti uniti
punti uniti
troviamo l’inversa ![]() da cui
da cui 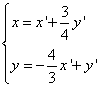
la retta y=mx+q deve trasformarsi in y’=mx’+q
![]() da cui
da cui ![]()
![]() da cui
da cui ![]()
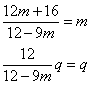
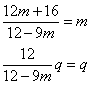
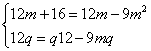
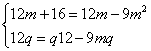 da cui
da cui
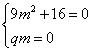 m=0 o q=0 non
soddisfano la prima equazione e quindi non ha rette unite.
m=0 o q=0 non
soddisfano la prima equazione e quindi non ha rette unite.
|
d) Stabilire se la centro-affinità trovata presenta rette unite. e) Calcolare l’area della figura trasformata del cerchio inscritto nel
trapezio in base alla centro-affinità trovata sopra. Considerando che se S e S’ sono le aree di due figure di
cui una è la trasformata dell’altra econsiderando che detA è il determinate
della trasformata si ha che
|
QUESTIONARIO
|
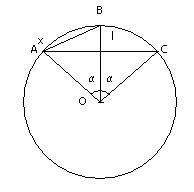
1) Nota la lunghezza di una corda di un cerchio di dato raggio,
calcolare quella della corda sottesa dall’angolo al centro uguale alla metà
di quello che sottende la corda data. [Nota – La risoluzione del problema è stata usata da
Tolomeo, II sec. d.C., per la costruzione di una tavola trigonometrica in
maniera equivalente alla nostra formula di bisezione del seno.]
2) Nello spazio ordinario sono dati due piani a , b
ed una retta r. Si sa che r è parallela ad a e perpendicolare a b . Cosa si
può concludere circa la posizione reciproca di a e b ? Fornire un’esauriente
spiegazione della risposta. Sicuramente a e b non sono paralleli altrimenti, per la proprietà
transitiva del parallelismo avrei che r è parallela con b il che è assurdo . Se s la retta intersezione con a e z la
retta intersezione con a e b ho
che per r è perpendicolare con z per ipotesi, e dato che r e s sono paralleli
, z è perpendicolare con s e quindi a e b sono perpendicolari. (teorema
delle tre perpendicolari ). 3) Il dominio della funzione f(x) = |
A) x£ 0 e/o x>2; B) x£ 0 e/o x³
2; C) x=0 e/o x>2; D) x=0
e/o x³ 2.
|
Una sola risposta è corretta: individuarla e fornire
un’esauriente spiegazione della scelta operata. La risposta è la D.
poiché il C.E. 4) Si consideri un polinomio di grado n³ 2 nella variabile reale x con coefficienti reali. Dimostrare che
condizione necessaria e sufficiente affinché esso ammetta due zeri uguali al
numero reale a è che il valore del polinomio e
quello della sua derivata prima si annullino per x=a . Se i polinomio ammette due zeri coincidenti allora è
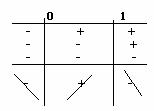
divisibile per il Quindi il teorema dice che Se Il polinomio ammette due zeri coincidenti allora considerando che la derivata è 5) Stabilire se esistono i limiti della funzione f(x) = |
a) x ® +¥ ; b) x ® - ¥ ; c) x ® 0 ,
e, in caso di risposta affermativa, determinarli.
Dato ![]() il campo di esistenza
diventa x>-1 con x diverso da 0.
il campo di esistenza
diventa x>-1 con x diverso da 0.
Esistono solo i limiti a) ![]() c)
c)![]()
|
6) Si consideri il seguente sistema di equazioni nelle incognite x, y,
z: |
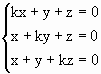
dove k è un parametro reale.
|
Dire se l’affermazione: «il sistema ammette la sola
soluzione x=0, y=0, z=0 per ogni valore di k diverso da 1» è vera o falsa e
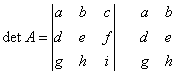
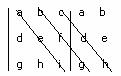
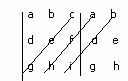
fornire una spiegazione esauriente della risposta. Per il teorema di Cramer se il detA è diverso da zero ammette una ed una sola
soluzione. Calcolando il determinate secondo la regola di Sarrus abbiamo che Si ha che Ricordiamo la
regola di Sarrus su un determinate 3x3:
e si considerano somma
del prodotto delle diagonali principali S=(aei)+(bfg)+(cdh) meno la somma delle prodotto delle diagonali secondarie D=(ceg)+(afh)+(bdi) e allora il determinate diventa
detA= S=(aei)+(bfg)+(cdh)-(ceg)-(afh)-(bdi) 7) Utilizzando il procedimento preferito, dimostrare la formula che
fornisce l’area della regione piana racchiusa da un’ellisse di semiassi noti.
Considerando l’ellisse generale
abbiamo che 8) In un piano riferito ad un sistema di assi cartesiani ortogonali
(Oxy) sono date le affinità di equazioni: |
x’ =
(a+1) x – b y + a , y’ = (a–1) x + 2 b y – 1 ,
dove a, b sono parametri reali.
Dimostrare che fra esse vi è una similitudine diretta e di
questa trovare il punto unito.
![]() da cui
da cui
Per essere una similitudine deve essere
Ricordiamo che una similitudine diretta è del tipo ![]() e che il rapporto di similitudine è dato da
e che il rapporto di similitudine è dato da ![]() allora
allora
![]() da cui
da cui ![]() da cui
da cui ![]()
![]()
il punto unito è ![]()
![]()
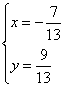
|
9) Un’urna contiene 30 palline uguali in tutto e per tutto fuorché nel
colore: infatti 18 sono bianche e 12 nere. Vengono estratte a caso, una dopo
l’altra, due palline. Qual è la probabilità che la seconda pallina estratta
sia bianca sapendo che la prima: |
|
a) è bianca e viene rimessa nell’urna? a) b) c) |
10) Considerata l’equazione in x:
a x2 + b x + c = 0 ,
dove a, b, c sono numeri reali qualsiasi, con a¹ 0, scrivere un algoritmo che ne determini le
soluzioni reali e le comunichi, esaminando tutti i casi possibili.
Se ![]() allora
allora ![]()
Altrimenti
Se ![]()
Se ![]() allora n.s.
allora n.s.
e ![]() allora
allora ![]()
![]()
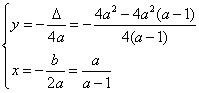 da cui
da cui